
Even interventions with large average benefits do not help everyone, which is a serious challenge for education policy in developing countries
While school enrolment in developing countries has increased remarkably over the past few decades, gains in learning have been much smaller (World Bank 2018). This 'learning crisis' means that, for example, three quarters of third-grade students in Kenya, Tanzania, and Uganda are still not able to comprehend a simple sentence (Uwezo 2016). Hundreds of studies aimed at understanding 'what works' to improve education have evaluated the causal effects of education interventions in developing countries. However, most have focused almost exclusively on the average effects of programmes. Across eight systematic reviews of the RCT literature on developing-country education programmes, there are just four mentions of how treatment effects might vary across students (Conn 2017, Evans and Popova 2016, Ganimian and Murnane 2014, Glewwe and Muralidharan 2016). Moreover, previous studies have solely focused on heterogeneity from observed characteristics such as gender or ability—leaving heterogeneity that cannot be explained by observed characteristics unexplored. Documenting variation in treatment effects is crucial for addressing the learning crisis, because programmes can have substantial average effects while still failing to help a large fraction of students.
Even an effective educational intervention leaves some children behind
In a new paper (Buhl-Wiggers et al. 2022), we study the heterogeneity of the impacts of one of the most effective education interventions in the world. The programme—the Northern Uganda Literacy Project (NULP)—focuses on improving mother-tongue (native-language) literacy in first- to third-grade classrooms in Northern Uganda. It provides teachers with scripted lesson plans and a slower-paced phonics-based curriculum to build foundational reading skills. The programme also involves integrated textbooks and intensive training and support for teachers (Kerwin and Thornton 2021). Our data cover the years 2014-2016 and come from a randomised experiment in 128 schools. The average treatment effect of the programme on literacy scores at the end of third grade is around 1.4 standard deviations of endline test scores, measured in the control group from the experiment. This makes it one of the very best educational programmes ever evaluated using a randomised control trial (e.g. McEwan 2015).
While the programme’s average treatment effect is huge, the effects vary sharply across students. Using classical statistical bounds from Fréchet (1951) and Höffding (1940), we estimate lower and upper bounds on the standard deviation of the treatment effects. Our lower-bound estimate of the standard deviation of the programme’s treatment effects is roughly 1.1 standard deviations of endline test scores. If we assume the treatment effects are normally distributed, then this means that 29% of students realize gains of over 2 standard deviations in endline test scores—but also that more than 10% of students are actually harmed by the programme, ending up worse off than they would have been without the intervention.
The variation in treatment effects can also be analysed using quantile treatment effects (QTEs). As illustrated in Figure 1, these show how much the programme shifts percentiles of endline test scores. The QTEs echo the finding of huge variation in the treatment effects from the Fréchet-Höffding bounds: the programme increases the 95th percentile of test scores by nearly 3 standard deviations, but leaves the 5th percentile nearly unchanged.
Figure 1 Quantile treatment effects on reading scores
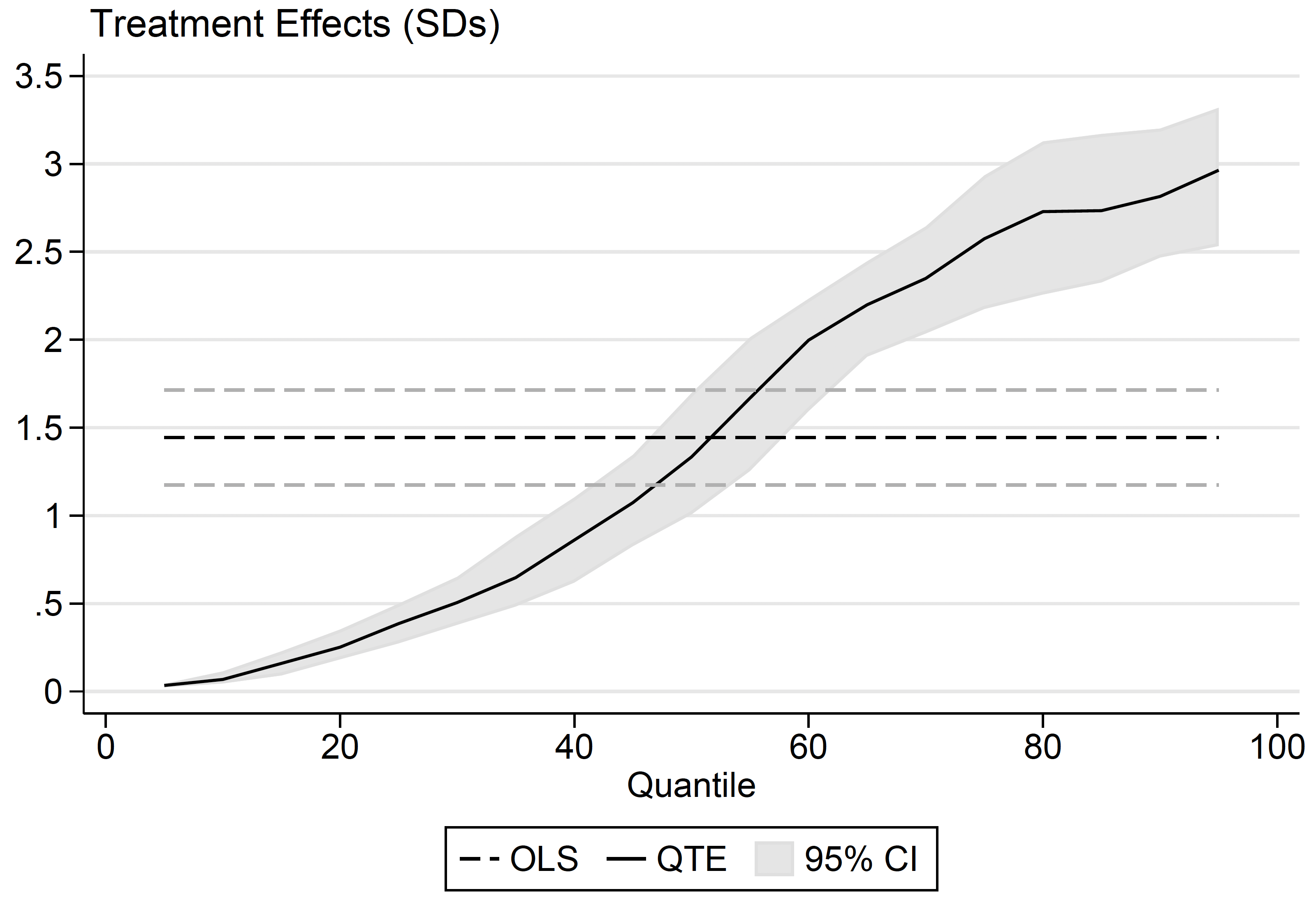
Notes: The dark dashed line is the average treatment effect, with the 95% confidence interval indicated via light dashed lines.
Which students are left behind? It is hard to say
Following Djebbari and Smith (2008), we divide the treatment effect heterogeneity into a 'systematic' component (the part explained with observed data) and an 'idiosyncratic' component (the part unexplained with observed data). If all the variation in treatment effects could be explained through observable characteristics, we could identify which students are left behind, and think about providing compensating interventions or improving the targeting of the original intervention.
To capture systematic variation, we apply two methods. First, we use the conventional approach of examining simple interactions between baseline variables and the treatment indicator in a linear regression. Second, we apply the machine-learning (ML) algorithm suggested by Chernozhukov et al. (2020). The conventional approach finds little correlation between treatment effects and student, teacher, or school characteristics. In contrast, the ML approach uncovers a meaningful relationship between treatment effects and baseline variables. Figure 2 shows the Sorted Group Average Treatment Effects (GATES), which separate the predicted treatment effects into quintiles (fifths of the overall sample) from the smallest to the largest effects. The five quintiles range from a treatment effect of less than 0.5 standard deviations to more than 2.0 standard deviations—a substantial range. None of the GATES are negative, and none are as high as the upper end of the effects that we get from the Fréchet-Höffding lower bound.
Figure 2 Sorted group average treatment effects (GATES)
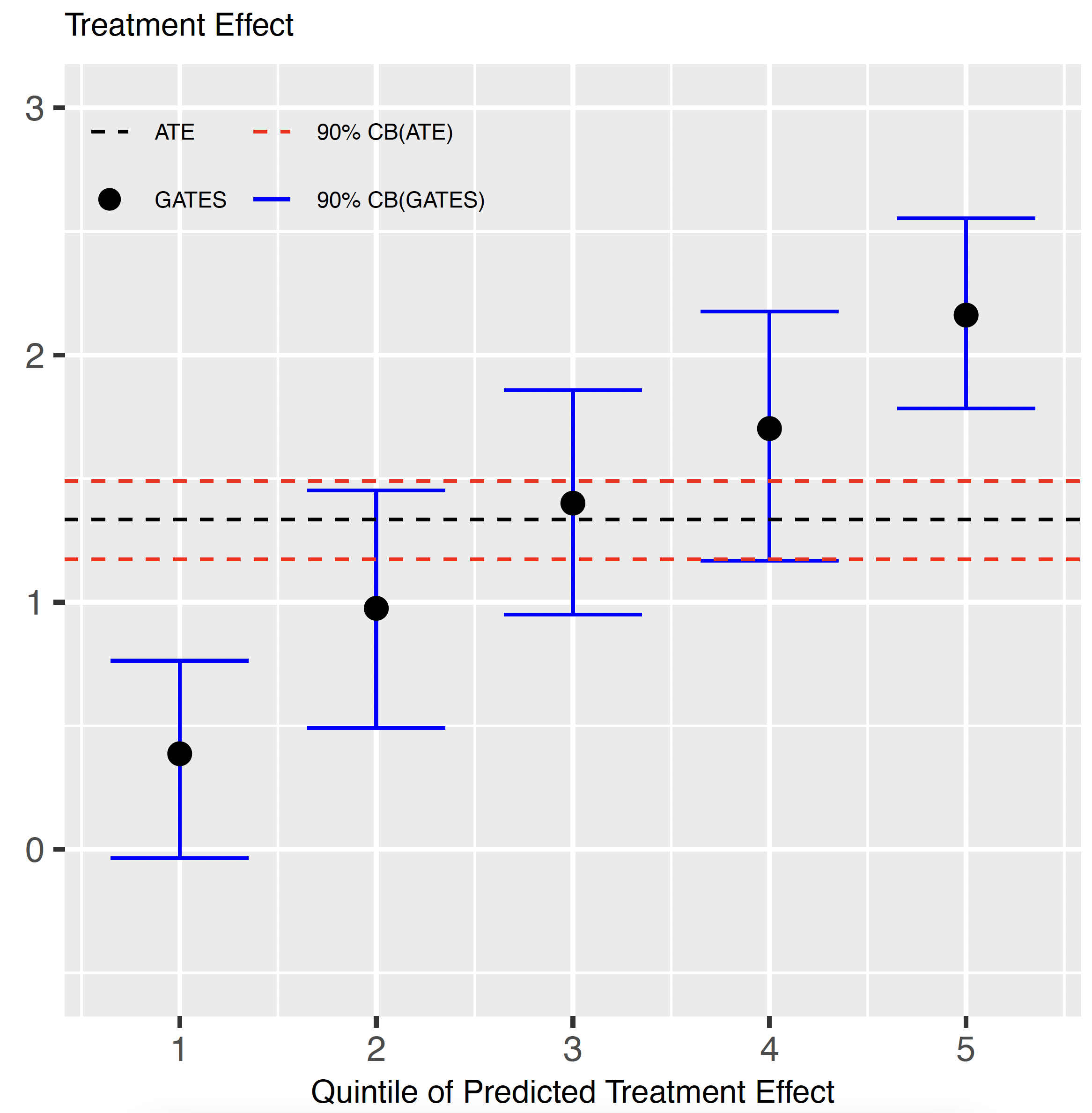
Notes: Sorted Group Average Treatment Effects (GATES) are estimated using the approach of Chernozhukov et al. (2020). Point estimates by ML proxy quintile and joint uniform 90 percent confidence intervals are estimated based on 50 random splits of the sample.
Moreover, the range of effects implied by the GATES is still much smaller than the range of treatment effects implied by the Fréchet-Höffding lower bound. Put differently, our analyses do little to capture the variation in treatment effects via observable student characteristics, even with ML techniques. The lower-bound standard deviation of treatment effects falls from 1.07 standard deviations under the unadjusted estimates to 1.05 if we remove systematic heterogeneity using conventional linear regressions. The ML approach does a bit better, but still leaves the lower bound at 0.99 standard deviations —less than an 8% reduction relative to the unadjusted case. To illustrate what these different estimates mean, Figure 3 presents the estimated percentage of students who are left behind—experiencing a negative treatment effect—under various scenarios. We estimate this share by using the Fréchet-Höffding lower-bound estimates of the standard deviation of treatment effects and imposing a normal distribution. The first bar shows that 9.5% of students are made worse off by the program. The second and third bars illustrate that ML techniques can explain away very little of this problem. Nearly 8% of students still experience negative treatment effects after subtracting off the systematic variation in treatment effects, and just 2.2% of the negative treatment effects can be explained by the ML approach. A large fraction of children are still left behind by the programme—without us understanding why.
Figure 3 Share of children left behind
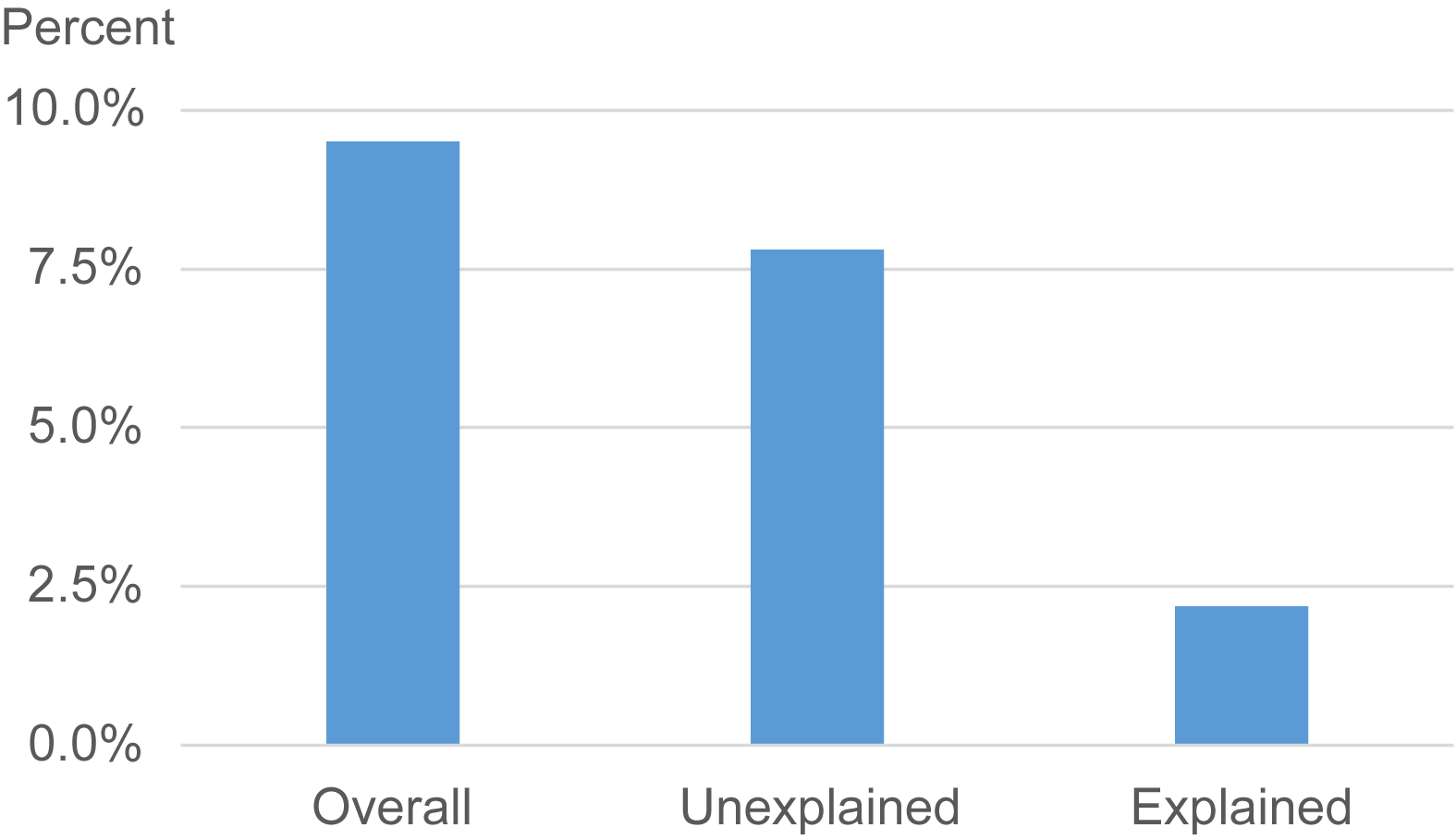
Notes: Figure displays the percentage of children who experience negative treatment effects if we use the Fréchet-Höffding lower bound on the standard deviation of the treatment effect and assume a normal distribution. The "Unexplained" bar uses the Fréchet-Höffding lower bound after removing systematic variation in the treatment effects via the machine-learning approach of Chernozhukov et al. (2020). The "Explained" bar shows the fraction of negative treatment effects that are explained away by the machine-learning method.
Even with an enormously effective intervention that on average helps students learn to read, some children are still left behind. Our findings also suggest that we are still far from understanding why education programmes have different effects across students. The NULP has highly varied effects on students’ test scores, but this variation cannot be explained through observed student characteristics. Answers to this question will come from both better theory and better data. Efforts to theoretically motivate and then collect a richer set of observed variables that capture the systematic treatment effect heterogeneity could help a great deal in understanding whether and why the effects of education interventions vary, and thus prevent children from being left behind. Studies of education interventions also must consider the distribution of treatment effects, rather than focusing exclusively on the average.
References
Buhl-Wiggers, J, J.T Kerwin, J Muñoz-Morales, J Smith, and R Thornton (2022), "Some Children Left Behind: Variation in the Effects of an Educational Intervention", Journal of Econometrics, Forthcoming.
Chernozhukov, V, M Demirer, E Duflo, and I Fernández-Val (2020), "Generic Machine Learning Inference on Heterogeneous Treatment Effects in Randomized Experiments, with an Application to Immunization in India", NBER Working Paper No. 24678.
Conn, K. M (2017), "Identifying Effective Education Interventions in Sub-Saharan Africa: A Meta-Analysis of Impact Evaluations", Review of Educational Research 87(5): 863–898.
Djebbari, H and J Smith (2008), "Heterogeneous Impacts in Progress", Journal of Econometrics 145(1): 64–80.
Evans, D. K and A Popova (2016), "What Really Works to Improve Learning in Developing Countries? An Analysis of Divergent Findings in Systematic Reviews", The World Bank Research Observer 31(2): 242–270.
Fréchet, M (1951), "Les Tableaux de Corrélation Dont les Marges Sont Données", Annales de l’Université de Lyon. Section A: Sciences, Mathématiques et Astronomie 14: 53–77.
Ganimian, A. J and R. J Murnane (2014), Improving Educational Outcomes in Developing Countries: Lessons from Rigorous Impact Evaluations, NBER Working Paper No. 20284.
Glewwe, P and K Muralidharan (2016), "Improving Education Outcomes in Developing Countries: Evidence, Knowledge Gaps, and Policy Implications", in E A Hanushek, S Machin, and L Woessmann (eds), Handbook of the Economics of Education 5: 653–743, Elsevier.
Höffding, W (1940), "Masstabinvariante Korrelationsmasse für Diskontinuierliche Verteilungen", Arkiv Für Matematischen Wirtschaften and Sozialforschung 7: 49–70.
Kerwin, J. T and R. L Thornton (2021), "Making the Grade: The Sensitivity of Education Program Effectiveness to Input Choices and Outcome Measures", The Review of Economics and Statistics 103(2): 251–264.
McEwan, P. J (2015), "Improving Learning in Primary Schools of Developing Countries: A Meta-Analysis of Randomized Experiments", Review of Educational Research 85(3): 353–394.
Stern, J, M Jukes, B Piper, J DeStefano, J Mejia, P Dubeck, B Carrol, R Jordan, C Gatuyo, T Nduku, M Punjabi, C.H.V Keuren, and F Tufail (2021), Learning at Scale: Interim Report, RTI International.
Uwezo (2016), Are Our Children Learning? Uwezo Uganda Eighth Learning Assessment Report, Twaweza East Africa.
World Bank (2018), World Development Report 2018: Learning to Realize Education’s Promise.





