
A new methodology combining experimental data with a quantitative model sheds light on the household-level and distributional effects of scaling up agricultural policies.
Roughly two-thirds of the world’s poor work in agriculture (Castaneda et al. 2016). Policy interventions aimed at increasing agricultural productivity – such as programmes that provide access, training, or subsidies for modern inputs and production techniques – have therefore been central in the fight against global poverty.
In a push for ‘evidence-based policymaking’, recent years have seen a surge of randomised or quasi-experimental evaluations designed to measure the impact of these agricultural policies (e.g. Magruder 2018, Caldwell et al. 2019). While rightly credited with revolutionising the field of development economics, these experiments often struggle to capture some of the important general equilibrium (GE) effects that can emerge as programmes are scaled up to a larger segment of the population. For example, changes in crop prices or local wages that may not occur in a small-scale experiment can meaningfully alter the impact of scaled-up policies on household real incomes and its distribution. On the flip side, more traditional ``computable GE’’ analyses have often lacked the causal identification that experimental approaches bring to bear, and have abstracted away from a realistic and granular economic geography of farm production, consumption, and trade costs that influences the propagation of local shocks through the economy (De Janvry et al. 1995).
In a recent paper (Bergquist et al. 2022a), we propose a new methodology for quantifying how the effects of local agricultural policy interventions differ when implemented at scale. This methodology can both complement and be informed by evidence from field and quasi-experiments. We showcase our approach by exploring the impacts of a subsidy for modern inputs (such as chemical fertilisers and hybrid seeds) in Uganda, and show how it can be combined with experimental results to harness the strengths of both approaches.
A new approach
We start by developing a quantitative model of farm production, consumption and trading, building on recent contributions in international trade and economic geography (Fajgelbaum & Redding 2014, Fajgelbaum and Redding 2022, Costinot and Donaldson 2016, Sotelo 2020, Farrokhi and Pellegrina 2022). Our model deviates from existing approaches to capture a number of important features that we document in this setting. This includes allowing for additive (per-unit) trade costs for agricultural goods (so that price changes are passed through differently across space), agricultural goods that are not differentiated across local markets (so that the model can capture the sparseness of market-to-market trade linkages observed in the data and their changes in response to shocks), household demand that may differ across real incomes (so that crop price changes may have meaningful distributional effects, as poor vs. rich households consume different bundles of goods), and technology adoption choices faced by farmers (allowing for more flexible production functions and richer margins of adjustment to policy shocks).
The model is granular enough to estimate the impact of policies at the level of individual households, allowing us to match the unit of observation often used in experiments, and to speak to distributional implications. We then develop a new solution method in this environment – to quantify changes in household outcomes in response to policy changes – that relies on rich but widely available microdata on household location, crop production and expenditure shares.
Combining experiments and model
We estimate the model's key demand and supply elasticities using exogenous variation in consumer and producer prices from existing field experiments (Bergquist and Dinerstein 2020, Carter et al. 2020). On the supply side, we also make use of a natural experiment that uses variation in world market crop prices that propagate differently to local markets in the presence of per-unit trade costs.
To calibrate trade costs, we make use of estimates from Bergquist et al. (2022b), using Ugandan market and trader survey microdata to provide information on market-to-market trade flows and crop prices at origin and destination across crops. We then use Ugandan administrative data on household location, production, and consumption to calibrate the model to the roughly five million households who populate the country.
The impact of agricultural policies at scale
We use the calibrated model to study how the effects of agricultural policies differ between a local intervention and one implemented at scale. We run two types of counterfactuals – alternative scenarios – for each of the roughly 4,500 rural parishes in Uganda. In each parish, we randomly select 2.5% of the local population (leading to a random national sample of roughly 100,000 households). We first quantify changes in household real incomes caused by an intervention that targets a 75% cost subsidy for modern inputs, but only at each of these local treatment groups, keeping the rest of Uganda unexposed (akin to implementing roughly 4,500 separate experiments). We then compare these local effects to the welfare changes experienced by the same sample of households under an intervention that scales the subsidy policy to all rural households in Uganda.
Pooling all local randomised interventions, we find that the average effect of the subsidy at a small scale is a 4.4% increase in household real income. This is driven mostly by farmers saving on costs for the subsidised inputs (and using more of them), while output and other input prices remain mostly unaffected. However, at scale, we find that the welfare effect for the same sample of farmers receiving the same intervention as in the local experiment changes by as much as +/-5 percentage points across households. Figure 1 presents these changes, plotting the difference in the effect of the intervention at scale versus in the local intervention for each household in the 100,000 national sample. We see these differences are large relative to the local treatment effect: over a third of households experience a change greater than +/-50 % of their local effect. On average, the at-scale intervention produces a smaller welfare effect by about 20%, with a 3.6 percentage point gain. However, not all households are worse off at scale: about 20% experience at-scale effects that exceed their gains from the local intervention.
Figure 1: Differences in welfare change (at scale – local) in percentage points across households
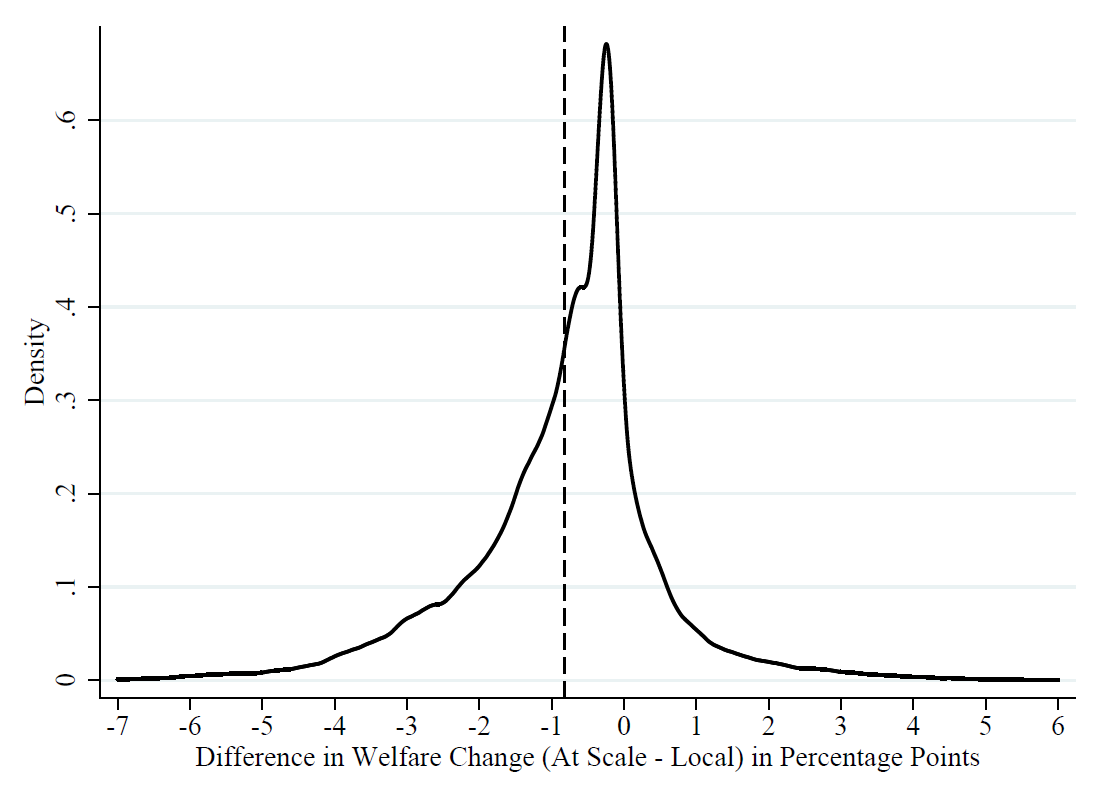
Notes: This plots the distribution of the difference in real income changes from at-scale versus local interventions in percentage points for the identical representative sample of roughly 100,000 randomly selected rural households.
The distributional implications underlying these differences are stark. Figure 2 presents the welfare impact of the subsidy in the local intervention (dashed line) and the at-scale intervention (solid line), as a function of initial land share in total income. We see that the local intervention is highly regressive: land-rich farmers experience much larger real income gains than land-poor farmers. In contrast, the at-scale intervention is much less regressive, with land-poor farmers doing better than under the local intervention, while the land-rich fare worse.
We find that this is driven mostly by income effects, rather than effects on the consumption price index. In the local intervention, the land-rich experience larger income gains from the subsidy, in part as they use modern inputs more intensively at baseline. However, at scale, GE effects on average decrease the price of input-intensive crops and increase the price of local labour. This reduces land-rich incomes by 2 percentage points and increases land-poor incomes by 1.5 percentage points.
Figure 2: Distributional Implications
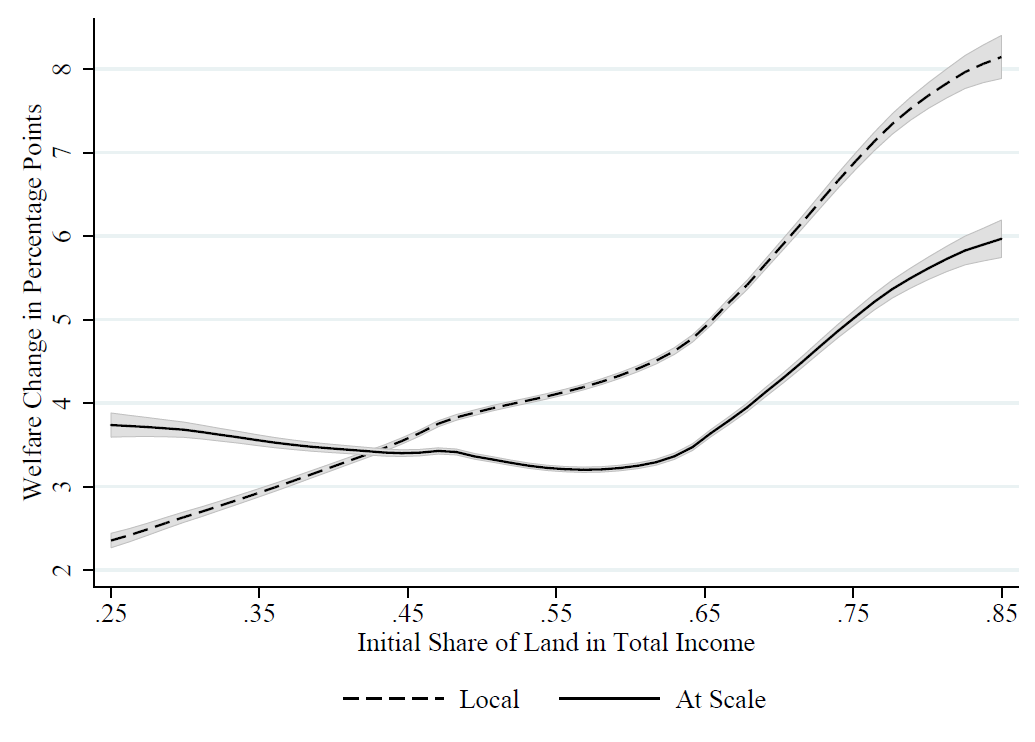
Notes: The figure plots the welfare changes resulting from the local and at-scale interventions, respectively, as a function of initial land income shares. Estimates are from local polynomial regressions based on the identical sample of roughly 100,000 rural Uganda households.
Implications for experimental approaches to estimating GE forces
We also use our framework to provide insights for experimental approaches to estimating GE effects. A growing literature employs ‘randomised saturation designs’, which randomise not only treatment across individuals, but also the saturation rate (share of individuals treated) across geographic areas (‘clusters’), to elicit GE effects with experimental variation (e.g. Baird et al. 2011, Burke et al. 2019, Egger et al. 2022). Due to constraints on statistical power and feasibility, such designs often limit the comparison to two discrete levels of saturation. In order to identify the impact of policies at scale (e.g. at 100% national saturation), one must thus typically extrapolate from these two points of saturation, subject to two important assumptions: i) GE forces are monotonic and roughly linear with respect to changes in the saturation rate; and ii) GE forces observed at the level of local clusters are representative of the effects of higher saturation at larger geographical scales (e.g. at the national level).
We use our approach to provide insight on the plausibility of these two assumptions. On the positive side, results suggest that the first assumption is plausible. We find that the average gains to the initially treated farmers in the local interventions decline close to linearly as a function of scale-up to the rest of the country.
However, our results suggest caution about the second assumption. Because it is nearly impossible to randomise nationwide saturation rates, experiments typically randomise saturation rates at some lower, sub-national level. In our setting, we find that increases in saturation at the national level decrease the average rural welfare gain. However, if we instead implement the same counterfactuals in steps of 10% of the population within sub-counties (a large but feasible unit for randomisation saturation), we find no change in average welfare gains, even at 100% saturation. These findings suggest caution when extrapolating from GE effects observed in designs that randomise saturation within smaller geographic units.
Combining toolkits for greater insight
The framework we lay out is aimed at providing a methodology that can be combined with field and quasi-experiments to investigate GE treatment effects at scale. In the paper, we include a discussion of practical considerations when combining these toolkits. We see these two approaches as complementary, with experiments providing strong causal identification of key parameters (and, if saturation is randomized as well, model validation), and our model-based approach providing quantitative estimates of counterfactuals that typically cannot be observed in experiments.
From a policy perspective, we show how different forms of scaling up agricultural policies can have varying average welfare effects and distributional implications. We hope that, in combination, the approaches we use can expand what can be learned from experiments or quantitative GE models alone.
References
Baird, S, C McIntosh, and B Ozler (2011), “Cash or Condition? Evidence from a Cash Transfer Experiment”, Quarterly Journal of Economics 126: 1709–1753.
Bergquist, L F, and M Dinerstein (2020), “Competition and Entry in Agricultural Markets: Experimental Evidence from Kenya”, American Economic Review 110(12): 3705–47.
Bergquist, L F, B Faber, T Fally, M Hoelzlein, E Miguel, and A Rodriguez-Clare (2022), “Scaling Agricultural Policy Interventions”, Working Paper.
Bergquist, L F, C McIntosh, and M Startz (2022), “Search Costs, Intermediation, and Trade: Experimental Evidence from Ugandan Agricultural Markets”, Working Paper.
Burke, M, L F Bergquist, and E Miguel (2019), “Sell Low and Buy High: Arbitrage and Local Price Effects in Kenyan Markets”, Quarterly Journal of Economics 134(2): 785-842.
Carter, M, R Laajaj, and D Yang (2020), “Subsidies and the African Green Revolution: Direct Effects and Social Network Spillovers of Randomised Input Subsidies in Mozambique”, American Economic Journal: Applied Economics 13(2): 206-29.
Castaneda, A, D Doan, D Newhouse, M C Nguyen, H Uematsu, and J Pedro Azevedo (2016), “Who are the poor in the developing world?”, World Bank Policy Research Working Paper.
Costinot, A and D Donaldson (2016), “How Large are the Gains from Economic Integration? Theory and Evidence from US Agriculture, 1880-1997”, NBER Working Paper 22946.
Costinot, A and A Rodriguez-Clare (2014), “Chapter 4 - Trade theory with numbers: Quantifying the consequences of globalization”, Handbook of International Economics 4: 197–261.
de Janvry, A and E Sadoulet (1995), Quantitative Development Policy Analysis, London and Baltimore: The John Hopkins University Press.
Egger, D, J Haushofer, E Miguel, P Neihaus, and M Walker (2022), “General Equilibrium Effects of Cash Transfers: Experimental Evidence from Kenya”. Econometrica 90(6): 2603-2643.
Fajgelbaum, P and S J Redding (2022), “External integration, structural transformation and economic development: Evidence from Argentina 1870-1914”, Journal of Political Economy.
Farrokhi, Farid, & Pellegrina, Heitor S. 2022. Trade, technology, and agricultural productivity. Forthcoming, Journal of Political Economy 130(5): 1249-1318.
Head, K and T Mayer (2014), “Gravity equations: Workhorse, toolkit, and cookbook”, Handbook of International Economics 4: 131-195.
Magruder, J (2018), “An Assessment of Experimental Evidence on Agricultural Technology Adoption in Developing Countries”, Annual Review of Resource Economics 10: 299-316.
Sotelo, S (2020), “Domestic trade frictions and agriculture”, Journal of Political Economy 128(7): 2690-2738.






